





















Université de La Réunion
Cours préparé par Dr Philippe Martin
http://www.phmartin.info/cours/ao/
(→ supports de cours, TDs, exemples de QCM, corrigés, ...)
Ce document est la version "slides" de la 1ère partie.
Sauf en cas d'ajout, toute différence
avec la version PDF
est une erreur typographique : si vous en voyez, merci de les signaler !
Dans ce document, pour naviguer vers une autre page, utilisez les flèches de
votre clavier
(ou la barre d'espace pour la page suivante).
L'aide en bas à gauche de cette fenêtre donne plus de détails.
| L'objectif de ce cours est de faire connaître à ses étudiants - les composants et principes majeurs de fonctionnement d'un ordinateur ou d'un réseau d'ordinateurs, depuis l'électronique (transistors, ...) jusqu'à la programmation, - les critères principaux d'évaluation de performance (capacité, rapidité, ...) - les termes français et anglais relatifs à tout ceci. |
Pile des objects/processus nécessaires au traitement automatique de l'information :
|
Ceci fait partie du rôle de l'étudiant. Note : le plus souvent, un enseignant ne
ne peut deviner ce que l'étudiant ne comprend pas si celui-ci ne l'exprime pas.

Vous n'avez pas à vous souvenir des dates exactes (ce serait du "par cœur")
mais vous devez avoir compris ce à quoi chaque terme réfère.
Préhistoire : calcul avec des cailloux (latin : calculi) ou des doigts (latin : digiti)
Vers -500, premiers outils de calcul manuels :
abaques, bouliers, règles à calcul

Diverses bases : 10 (doigts), 12 (heures), 60 (temps, angles), 7 (musique), ... À lire : 1 (Système sexagésimal), 2 (compter sur ses doigts en duodécimal/binaire) et 3 (avantages d'autres bases que 10)
Numération positionnelle : chaque chiffre a un poids dans une base, e.g., 1803 = 1*103 + 8*102 + 0*101 + 3*100 = 1*1000 + 8*100 + 0*10 + 3*1 → nécessite le chiffre 0 (inventé/connu par certains savants et commerçants indiens et arabes 2 siècles après J.C. ; adopté par certains Européens au 11ème siècle)
Numération romaine, e.g., MDCCCLXXIIIromain = 187310
1614 : tables de logarithmes de John Neper

1632 : invention de la règle à calcul (Oughtred) et Francis Bacon invente le premier codage de l'alphabet
1642 : Blaise Pascal créé la Pascaline qui additionne et
soustraie des nombres de 6 chiffres
(roues codeuses + notion de décalage des retenues)

1673 : Leibniz étend la Pascaline pour les 4 opérateurs (+, -,*,/). Il invente aussi le système binaire moderne ainsi que le calcul différentiel et intégral
1805 : Joseph Jacquard utilise des cartons troués (1ères cartes perforées) pour "programmer" les métiers à tisser
1833 : Charles Babbage débute la conception théorique de la Machine Analytique (→ 4 opérations arithmétiques de base) puis de la Machine Analytique, 1er modèle de calculateur programmable : - 4 parties : mémoire, unité de calcul, entrée (lecteur de cartes perforées), sortie (perforation) - 4 opérations arithmétiques, test et branchement conditionnel → en 1840, Ada Augusta Byron (fille du poète Lord Byron) invente et écrit les premières itérations successives (-> algorithme; 1ers programmes informatiques non exécutés)
1854 : Georges Boole publie l'algèbre booléenne (calcul sur les valeurs booléennes : Vrai et Faux)
1890 : Hermann Hollerith construit un calculateur de statistiques à cartes perforées, l'utilise pour le recensement américain, et fonde la Tabulating Machines Company qui devient IBM en 1924

1938 : conception de la Machine de Turing qui modélise/formalise les principes élémentaires du fonctionnement de toute machine et de toute opération mentale
1940 : invention du circuit imprimé (plaquette comportant des pistes pour relier les composants)
1920-1944 : calculateurs électro-mécaniques avec relais ou tubes (~ implémentations de "machines de Babbage")
début 1945 : ENIAC, 1er calculateur électronique programmable mais
nécessitant de rebrancher des centaines de câbles pour chaque calcul
car sa mémoire interne était trop petite; 1ers "bogues" (→ bug = insecte)
Le terme "calculateur électronique programmable" n'est pas utilisé
pour référer – entre autres – aux ordinateurs, il est utilisé pour référer aux
"ancêtres des ordinateurs" qui étaient déjà des calculateurs électroniques
programmables, e.g. l'ENIAC. Page qu'il n'est pas obligatoire de lire : 1

fin 1945 : EDVAC, 1er véritable ordinateur (→ programme en mémoire) → en 2025, l'ordinateur a 80 ans !
fin 1945 : publication de la machine de von Neumann : unité arithmétique et logique (UAL) + unité de commande + mémoire centrale + unité d'entrée + unité de sortie
1947 : invention du transistor (Bell Telecom)
1949 : EDSAC, 1er véritable ordinateur suivant la "machine de von Neumann" (mais on peut considérer que l'ENIAC avait aussi un tel modèle)
Deux petits extraits de "Timeless S1-E8 (Space Race)" montrant le matériel informatique pilotant la mission Apollo 11 (1969) : - extrait 1 : une mémoire de 2 mégabytes ! - extrait 2 : ruban perforé, "interpretative opcode", "fixed-point arithmetic"
1950-1960 : ordinateurs de 1ère génération (électrique), basés sur des tubes à vides ; 1ères mémoires de masse (mémoires magnétiques, accès séquentiel)
1960-1970 : 2ème génération (électronique), basés sur des transistors ; mini-ordinateurs ; disques durs (accès direct); 1ers SGBDs [DBMSs] (système de gestion de bases de données) ; 1ers circuits intégrés ; 1ers langages de programmation (1960 : Lisp, Cobol, Fortran ; 1964 : Basic)
1970-1980 : 3ème génération (micro-électronique), basés sur une puce
(circuit intégré basé sur un microprocesseur) intégrant des milliers de
transistors ; 1ers ordinateurs personnels;
1er systèmes d'exploitation multi-utilisateurs : Multics (1969), Unix (01/01/1972)
1971 : Arpanet (ancêtre d'internet)
1972 : Intel sort le 8008 (8 bits, 200 KHz, 3500 transistors)
1974 : François Moreno invente la carte à puce

1980-1990 : - 4ème génération (puce intégrant des centaines de milliers de transistors) - ordinateurs personnels ; périphériques (souris, CD-ROM, ...) ; internet - 1980 : une branche de IBM adopte le futur MS-DOS (développé, abandonné, et vendu à MicroSoft par une autre branche de IBM) → monopole des logiciels de Microsoft sur la machine la plus vendue - 1991 : Linus Torvalds créé Linux en ré-écrivant/allégeant le noyau d'Unix
1990-... : - parallélisme (dansl e microprocesseur, plusieurs microprocesseurs - mémoires - WWW (1990 : réseaux de documents liés par des liens hypertextes; ce "Web" est différent de internet qui, lui, est un réseau de communication via des câbles, des ondes, ...) - début de la fusion de l'informatique, des télécommunications et du multimedia (1999 : iBook).
20ème siècle : siècle de la physique, chimie, ... et de l'informatique
21ème siècle : siècle de la physique, biologie, ... et de l'informatique ;
ordinateur électronique+photonique+quantique+biologique ?
À lire : "Informatique naturelle", "Ordinateur biologique", e.g., à ADN [1, 2]
1965 : Gordon Moore remarque que "le nombre de transistors intégrables
sur une puce de circuit intégré double tous les 18 (à 24) mois"
→ loi de Moore ("loi/observation empirique" : vérifiée de 1971 à 2021) :
la puissance des nouveaux microprocesseurs (pas celle de leurs CPUs)
et la capacité des nouvelles mémoires
doublent tous les 18 mois au plus (entre 12 et 18 mois).
La progression s'affaiblit et cette loi n'est plus exacte en 2025
mais, pour les évaluations, c'est l'énoncé ci-dessus qui est à retenir.
Allez sur Wooclap (depuis
"ao1wooclap" sur la
page Moodle du cours)
pour la question d'évaluation suivante (1 seule réponse à sélectionner) :
Selon la loi de Moore, la puissance des microprocesseurs ...
A) quadruple tous les trois ans (environ / au plus)
B) quintuple tous les trois ans (environ / au plus)
C) double tous 9 mois (environ / au plus)
D) triple tous 18 mois (environ / au plus)
E) aucune des 4 dernières réponses n'est juste
3.1. Définitions (rappel)
3.2. Codes numériques
3.2.1. Entiers positifs
3.2.1.1. Changement de base
3.2.1.2. Énumération
3.2.1.3. Addition
3.2.1.4. Unités
3.2.2. Entiers signés en binaire
3.2.3. Nombres fractionnaires en binaire
3.3. Codes non numériques (pour décimaux, caractères, ...)
("non numérique" dans le sens "non basé sur la numération positionnelle")
3.3.1. Codes pour caractères
3.3.2. Sérialisation des caractères : endianisme
3.4. Avantages du numérique par rapport à l'analogique
Sur Wooclap, pour évaluer votre compréhension des notions du plan ci-dessus
(rappel : 1 seule réponse juste) :
La numérisation est la représentation ...
A) d'un chiffre (seulement)
B) d'une donnée avec un code numérique (seulement)
C) d'une donnée avec un code numérique et non numérique
D) d'une donnée avec, possiblement, un code non numérique
E) d'une donnée avec un nombre (i.e. un code numérique ou non numérique)
F) les 2 dernières réponses sont justes
20=1 21=2 22=4 23=8 24=16 25=32 210=1024
216=210+6=210*26=1024*64=65536
2-1=0,5 2-2=0,25 2-3=0,125 2-4=0,0625
8-1=0,125 16-1=0,0625
décimal binaire octal hexadécimal 0 0 0 0 1 1 1 1 2 10 <- 2 2 3 11 3 3 4 100 <- 4 4 5 101 5 5 6 110 6 6 7 111 7 7 8 1000 <- 10 <- 8 9 1001 11 9 10 <- 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D 14 1110 16 E 15 1111 17 F 16 10000 20 10 <-
Cette table est à comprendre (pas à apprendre/copier → contre-productif).
A) 118
B) 910
C) 135
D) les 3 dernières réponses (sont justes)
E) aucune des 4 réponses précédentes (n'est juste)
A) 7650108 B) 1752028 C) 1762028 D) 1751028 E) aucune des 4 réponses
(cette page est – pour vos notes dans ce cours d'AO – la plus importante
de ce cours car de nombreuses questions de ce cours sont
directement ou indirectement liées à cette page)
Avec 1 bit (→ avec 1 chiffre en base 2),
on peut représenter 21 entiers : 0 et 1.
Avec 2 bits, on peut représenter
22 entiers :
002, 012, 102, 112.
Avec 3 bits, on peut représenter
23 (= 8) entiers : 0002, ... 1112.
Cf. page suivante pour 4 bits.
Ces notions sont évaluées plus de 50 fois dans ce cours (TDs, questions, ...).
Malgré cela, une bonne partie de vos prédécesseurs des années passées
n'y ont pas prêtés attention et leur taux de réussite pour les questions
relatives à ces notions est resté faible.
Comme illustré dans la page précédente, (les adresses d')une mémoire se
représente(nt) souvent avec le plus grand nombre en haut. C'est la convention
dans ce cours. Pour les tables de vérité, c'est souvent l'inverse (elles seront
utilisées dans les parties 3 et 4 du cours).
Dans les deux cas, la technique d'énumération est la même.
Ci-dessous : 5 exemples, de "avec 0 bit" jusqu'à "avec 4 bits",
avec les plus grands nombres en bas.
Notez que chaque exemple se construit en reprenant le précédent 2 fois
(d'où le nombre total de 2nombreDeBits entiers/mots/... dans chaque exemple) :
une fois en le préfixant par des "0", une fois en le préfixant puis par des "1".
0 bit 1 bit 2 bits 3 bits 4 bits
0 00 000 0000
1 01 001 0001
10 010 0010
11 011 0011
100 0100
101 0101
110 0110
111 0111
1000
1001
1010
1011
1100
1101
1110
1111
Exemples de question d'évaluation :
w@ = w. = 0 = 002 = 08 = 02
@w@ = .w. = 1 = 012 = 18 = IR
@@w@ = ..w. = 2 = 102 = 28 = IIR
@@@w@ = ...w. = 3 = 112 = 38 = IIIR
....w. = 4 = 1002 = 48 = IVR
.....w. = 5 = 1012 = 58 = VR
... ...w. = ......w. = 6 = 1102 = 68 = VIR
. ... ...w. = .......w. = 7 = 1112 = 78 = VIIR
.... ....w. = ........w. = 8 = 10002 = 108 = VIIIR
.... ....w. = .........w. = 9 = 10012 = 118 = IXR
..... .....w. = ..........w. = 10 = 10102 = 128 = XR
. ..... .....w. = ...........w. = 11 = 10102 = 138 = XIR
Pour montrer sa compréhension/interprétation des notions de ce texte (ce message),
12 = .... .... ....w. = 11002 = 1'1002 = 148 = XIIR
X 1101'10012 Y 1001'00102 X+Y 1'0110'10112
Si les registres ou mots-mémoire d'une machine sont de
1 octet [byte] (8 bits),
comme X+Y doit normalement s'étendre sur 9 bits,
le processeur ne conserve que 0110'10112 mais
signale au programmeur un "dépassement de capacité" [overflow].
Notes :
1) dorénavant, les réponses proposées pour les questions d'évaluation
sur Moodle sont automatiquement mélangées, lorsque possible ;
2) suivant le temps restant, les questions suivantes sont à effectuer
maintenant ou au début du 1er TD.
De même (cf. Wikipedia's Préfixe binaire et Metric prefix) :
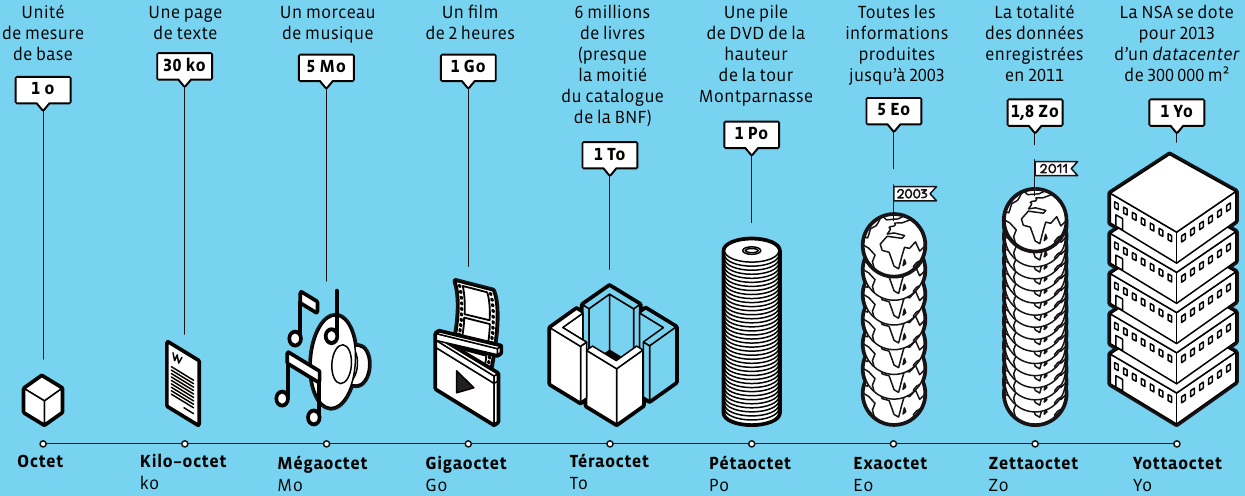
Pour plus de détails, lisez le chapitre "La déferlante des octets" (pp. 20-27) du
"journal du CNRS No262, nov.-dec. 2012". La figure ci-dessus en est extraite.
En 2010, Eric Schmidt (PDG de Google de 2001 à 2011) affirmait :
Tous les deux jours, nous produisons autant d'informations que
nous en avons générées depuis l'aube de la civilisation jusqu'en 2003.
Non obligatoire de regarder :
1. vidéo sur ce qui existe physiquement à différentes échelles de grandeurs
2. le bug de l'an 2038
Questions liées aux puissances de 2 sur Wooclap :
* Supposez que vous ayez une bande de papier-toilette de 1024 mètres de long
et que vous puissiez la plier en deux (parties égales et parfaitement plates) 12
fois de suite (→ ?? couches), quelle longueur obtiendriez-vous en centimètres ?
(largeur constante ; pliures supposées parfaites : non arrondies, ...)
Notes : 1) le record avec du papier du type "papier-toilette" est bien
de 12 fois, avec une longueur initiale de 1219m, en 2002, par une lycéenne de
16 ans qui trouva préalablement la formule lui permettant de calculer la
longueur nécessaire en fonction de l'épaisseur du papier le plus fin qu'elle
avait trouvé ;
2) si vous pouviez plier 42 fois une feuille de papier, vous
obtiendriez une épaisseur environ égale à la distance Terre-Lune.
* Question(s) liée(s) à l'isopoint génétique (pour culture : 1, 2 et 3)
Exemple : représentation en binaire de
+7 (= 01112) et de -7 (= ????2)
Trois méthodes principales
(que nous allons voir et qui donnent des résultats différents) :
Le bit le plus à gauche représente le signe (1 : négatif ; 0 : positif).
Les autres bits représentent la valeur absolue de l'entier signé.
Peu utilisé car avec cette méthode
De manière générale (pas seulement pour cette sous-section), une suite de
bits (ou de chiffres) ne peut être interprétée par l'homme ou la machine tant
que son type (e.g., entier, caractère(s), nombre fractionnaire avec
représentation par virgule flottante, image au format JPEG, ...) et le nombre de
bits utilisés ne sont pas précisés par ailleurs (e.g., via le typage de variables
dans programme et les sortes d'encodage utilisés par chaque machine pour
chaque type).
Dans ce cours, ces précisions sont données via le contexte (titre de la section,
sujet de l'exercice, ...) et/ou dans les indices comme ci-dessus.
Si un nombre est en base 10 ou s'il s'agit d'un entier positif, il est optionnel de
préciser cela : ce seront des précisions "par défaut".
De manière similaire, pour les entiers positifs il est inutile de préciser le
nombre de bits.
Pour les nombres négatifs, le nombre de bits sera supposé être celui impliqué
par le nombre de chiffres utilisés dans ces nombres.
Ainsi, dans les exemples ci-dessus, les parties en italique sont facultatives.
Soit x un entier positif qui nécessite au moins n bits pour sa représentation en binaire,
"bin" une fonction qui renvoie la représentation binaire d'un nombre,
complément_à_2(x) le complément à 2 de bin(x)
qui peut être utilisé pour représenter -x en binaire, et
complément_à_1(x) le complément à 1 de bin(x)
qui peut aussi être utilisé pour représenter -x en binaire
complément_à_2(x) = bin(2n - x)
= bin((2n - x - 1) + 1)
= bin(2n - 1 - x) + 1 = complément_à_1(x) + 1
Complémenter à 1 revient à changer tous les 0 en 1, et vice versa.
Exemples sur 4 bits (résultats différents avec 3 bits ou 5 bits) :
complément_à_2(110) = complément_à_1(00012) + 1
= 11102(complément à 1 sur 4 bits) + 1
= 11112(complément à 2 sur 4 bits)
= -110(complément à 2 sur 4 bits)
//note : 11112 = 1510(entier positif)
complément_à_2(710) = complément_à_1(01112) + 1
= 10002(complément à 1 sur 4 bits) + 1
= 10012(complément à 2 sur 4 bits)
= -710(complément à 2 sur 4 bits)
//note : 10012 = 910(entier positif)
complément_à_2(810) = complément_à_1(10002) + 1
= 01112(complément à 1 sur 4 bits) + 1
= 10002(complément à 2 sur 4 bits)
= -810(complément à 2 sur 4 bits)
//note : 10002 = 810(entier positif)
Pour le "complément à 2" (complément arithmétique ; cf. notes ci-dessus),
comme pour le "complément à 1" (complément restreint ou logique),
soustraire deux termes <=> additionner le premier terme au complément
(arithmétique/logique).
Exemples sur 3 bits :
décimal signe+val.abs. compl. à 1 complément à 2 +4 100 100 100 +3 011 011 011 +2 010 010 010 +1 001 001 001 +0 000 000╮ 000 -0 100 111╯ +1 = (1)000 -1 101 110 +1 = 111 -2 110 101 +1 = 110 -3 111 100 +1 = 101 -4 ---(100) ---(011) +1 = 100
Ainsi : -0 = 1112(complément à 1 sur 3 bits) = 0002(complément à 2 sur 3 bits)
Quelle "expression sur les bits en C" calcule la puissance de deux maximum
qui divise un entier quand les entiers signés utilisent un complément à deux ?
Exemples :
0,012 = 0*20 + 0*2-1 + 1*2-2
= 0*1 + 0*0,510 + 1*0,2510
= 0,2510
0,12510 = 0,0012 car ((0,125 * 2) * 2) * 2 = 1
Représentation en machine classique (pas via des
"nombres universels", ni par
codage+calcul sur des rationnels ,
ni par "précision-infinie|multi-précision en
stockant les nombres via des tableaux de chiffres →
le BigInt de JavaScript") :
Représentation des réels normalisée au format IEEE 754 → 3 choix :

Plus précisément, E est appelé "exposant réel". Ce qui est stocké (sur n bits)
est appelé E', l'exposant "biaisé". Généralement, E' = E + (2n/2 -1) pour que
E' soit un nombre positif (→ 1 seule méthode d'encodage). E.g., sur 8 bits, le
biais, 2n/2 - 1= 127, les valeurs possibles de E vont de -127 à 128
(→ palette
équilibrée de nombres positifs et négatifs ; cf. TD) et les valeurs possibles de
E' sont entre 0 et 255 (on dit que E' est biaisé à 127). Note : dans la correction
du TD, un biais de 128 (au lieu de 127) est utilisé, ce n'est pas usuel. Pour les
QCMs, le biais sera de 2n/2 - 1 (donc 127 lorsque E est sur 8 bits).
C'est pourquoi, dans l'exemple ci-dessus, d'après le paragraphe précédent et la
page précédente : E' = E +127 = 2 + 127 = 129 = 128 + 1 = 1000 00012
Dans les programmes, les "flottants" sont des représentations des réels.
Leur précision étant limitée, les opérations sur les flottants peuvent être
fausses (e.g., "0,2 + 0,3 = 0,5" est faux dans les flottants) et ceci conduit à
des bogues [bugs] →
"Écran Bleu de la Mort" de Windows,
explosion de
la 1ère fusée Arianne 5, ... ;
cliquez ici pour un peu de théorie.
Il faut donc être prudent : ordonner/simplifier les opérations pour réduire les
erreurs et gérer l'accumulation des erreurs ou prouver que le programme
n'en génère pas (-> enseignements dans les années suivantes).
Exemple de question d'évaluation : Dans une gestion normalisée de
nombres en "virgule flottante" sous la forme M * BE, ...
A) au moins un nombre à gauche de la virgule est toujours représenté
physiquement (→ stocké) dans la mantisse
B) la représentation de E et M se fait généralement(mais pas dans le
cas où le format IEEE 754 est utilisé) par "signe et valeur absolue"
C) l'exposant est biaisé à 128 si représenté sur 8 bits au format IEEE 754
D) les 3 dernières réponses E) aucune des 4 dernières réponses
Les codes sont soit numériques, soit non numériques.
Nous venons de voir des codes numériques pour des nombres.
Les codes non numériques sont basés sur des tables.
Ils peuvent être pour des décimaux, des caractères, ...
Il existe de nombreux codes binaires non numériques pour décimaux.
En voici quelques uns.
Exemple de question d'évaluation : Le code biquinaire ...
A) est un code non numérique B) est un code sur 5 bits
C) a exactement 2 bit à 1 dans les 2 positions de gauche
D) les 3 dernières réponses E) aucune des 4 dernières réponses
Voici quelques codes binaires non numériques pour caractères
– alphanumériques (A..Z, a..z, 0..9), spéciaux (?,!, @, ", ...), etc. – :
Exemple de question d'évaluation : L'Unicode ...
A) est un code numérique B) inclut le code ASCII et le code EBCDIC
C) inclut les langues d'Asie dans sa sous-catégorie UTF-16
D) les 3 dernières réponses E) aucune des 4 dernières réponses
Sur Wooclap :
À quoi réfère l'expression "little-endian" ?
A) à une méthode qui consiste à commencer par "le petit bout"
B) au stockage des octets (d'une valeur multi-octets) dans l'ordre des poids
C) au stockage des octets normalement utilisé après le caractère UTF-16LE
D) les 3 dernières réponses
E) aucune des 4 dernières réponses
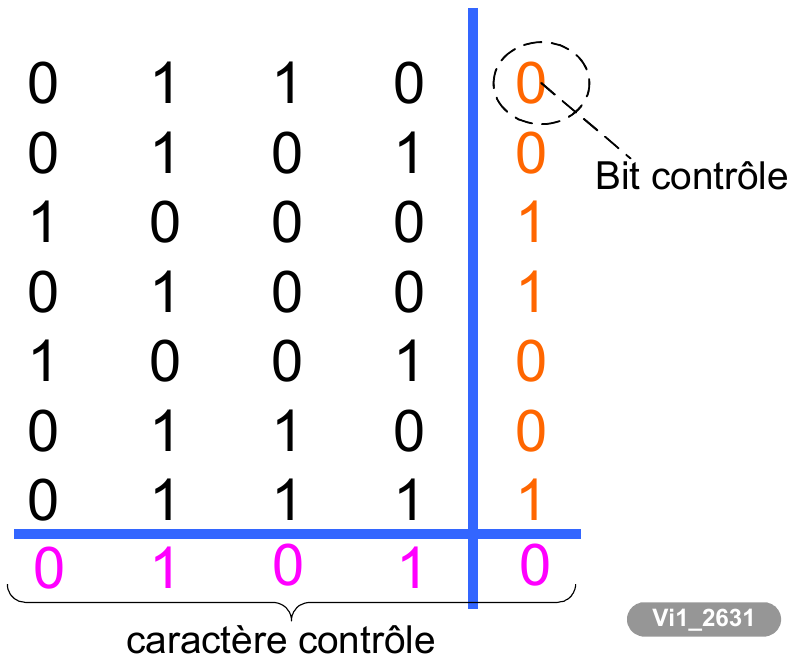
Mais les entrées-sorties des processeurs sont souvent en analogique
→ nécessité de convertisseurs entre numérique et analogique.
Sur Wooclap :
Les avantages du numérique par rapport à l'analogique sont ...
A) sa facilité d'implémentation B) sa fiabilité
C) sa faible sensibilité aux déformations du signal dues au magnétisme
D) ses possibilités supplémentaires de manipulation
E) les 4 autres réponses
Un domaine impliquant nécessairement de l'encodage en binaire est ...
A) la numérisation B) l'informatique
C) l'architecture des ordinateurs
D) les 2 dernières réponses E) aucune des 4 autres réponses
Rendu d'une image avec différentes précisions/définitions/compressions :

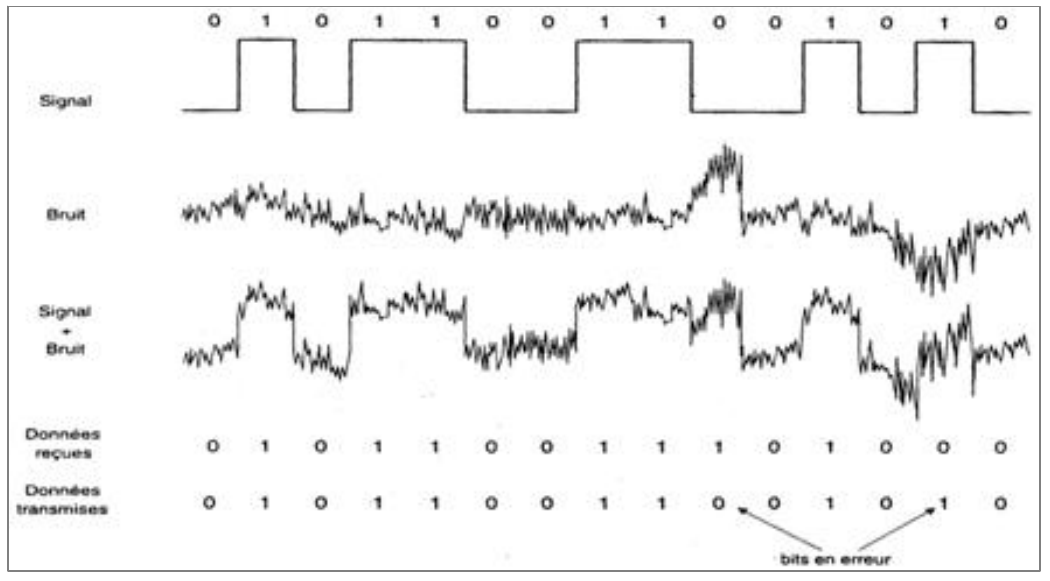
Effet du bruit sur un signal :
Si la section "3.2.1. Entiers positifs" de la partie 1 n'est pas finie,
ce TD commencera par finir cette section.
Il y aura en fait 2 "TDs réels" pour ce "TD pour la partie 1" (et, durant ceux-ci,
quelques questions Wooclap via "ao1wooclap" sur Moodle).
Pour chaque exercice (question Wooclap ou pas), un étudiant passera au
tableau pour l'effectuer et l'exercice sera corrigé au tableau.
I. Exemples de questions de contrôle pour le début du 1er TD réel
Un exemple de chiffre ni octal ni binaire est ... a) 0 b) 2 c) 5 d) 8 e) aucune des autres réponses
Quel est le plus grand chiffre (en base 10) entre 1 et 20 (inclus) ? ("plus grand": supérieur dans l'ordre des entiers naturels, e.g., 1 est plus grand que 0)
1010 est égal à ... a) 11002 b) 10102 c) 118 d) 1116 e) aucune des autres réponses
101012 est égal à ... a) 2110 b) 2310 c) 1716 d) 2116 e) aucune des autres réponses
L'addition des représentations en base 2 de 2510 et 1410 donne ...
Exprimer dans les bases suivantes le nombre de minutes dans "1h04min" (1 :04) : 10, 60, 30, 2, 8, 16.
II. Exemples de questions de conversion/calcul
(si cela n'a pas encore été fait, le début de la section 3.2.3 et la section 3.2.2 seront
présentées ; les questions après la 7.a sont optionnelles )
Exprimer en binaire, en octal et hexadécimal les nombres réels suivants : 32,625 et 128,75.
Convertir en décimal les nombres suivants, la base étant indiquée en indice : DADA,C16, 270,148 et 11011,011112
Donner, sur 8 bits, les représentations "signe + valeur absolue", "complément à 1" et "complément à 2" des valeurs décimales suivantes : -32 et -128.
Faire, en binaire puis en décimal, l'addition de 0018 à 3778 puis de 1778 à 2008, en supposant tout d'abord que 3778 et 2008 sont des représentations sur 8 bits en complément à 1 de nombres négatifs, puis en supposant que ce sont des représentations sur 8 bits et en complément à 2 de nombres négatifs.
On dispose d'une machine où les nombres réels sont représentés sur 32 bits (numérotés de droite à gauche de 0 à 31) avec : - une quantité fractionnaire sur 23 bits (les bits 0 à 22) correspondant à la mantisse m normalisée (0,5 =< m < 1) ; - un exposant biaisé, représentant une puissance de 2, codé sur 8 bits (les bits 23 à 30) ; - un bit pour le signe de la mantisse (0 si m >= 0, 1 si m < 0). Donner, sous la forme ±a * 2b (a et b décimaux), la valeur qui correspond aux 32 bits suivants (sous forme octale) : 27632000000.
La représentation des nombres réels correspond à celle décrite précédemment, sauf que le premier bit de la mantisse normalisée, premier bit qui est donc toujours à 1, n'est pas représenté sur la machine. Cet artifice complique un petit peu les manipulations mais permet de gagner en précision. Donner, sous forme octale, la représentation, sur une telle machine, des nombres décimaux suivants : 278 et -6,53125.
Soit une machine où les nombres réels sont représentés sur 12 bits, numérotés de droite à gauche de 0 à 11, avec : - une mantisse m normalisée (0,5 =< m < 1) sur 7 bits (les bits 0 à 6) ; - un exposant biaisé, représentant une puissance de 2, codé sur 4 bits (les bits 7 à 10) ; - un bit pour le signe de la mantisse (le bit 11). a) Trouver l'intervalle fermé des valeurs strictement positives représentables sur cette machine. Les bornes seront mises sous la forme ±a * 2b , a et b étant des entiers décimaux. Simplifier autant que possible. b) Mettre sous la forme ±a * 2b, où a et b sont des entiers décimaux, les 2 nombres réels suivants donnés sous forme hexadécimale : X=AE8 et Y=9DO. c) Calculer Z = y - X. Mettre le résultat sous la forme ±a * 2b, entiers décimaux, en simplifiant au maximum. d) Donner, sous forme octale, la représentation correspondant au nombre décimal suivant : -32,625.
Que représente en décimal l'information 377240000008 si on la considère comme un nombre entier, en complément à 1, en complément à 2 et comme un nombre réel, avec une représentation analogue à celle décrite dans l'exercice 7 ?